Polynomial Regression for Different Scores

Many research questions are intended to addressed by different scores, such as:

• Can patients provide self-psychological evaluations that agree with psychology professionals’ ratings? 
• How well do the attributes of teachers fit the needs or desires of the students?
•  Are values of the supervisors of an organization match the values of the subordinates?
• What are the degrees of similarity between perceived stigma of mental ill patients and their caregivers? 

We can start answering the questions by looking at the fit, similarity or agreement between two constructs as a predicting factor (Edwards, 1994). However, different scores can be problematic if we do not handle them in a right way. For instance, different scores are less reliable than either of their component measures. Moreover, people often reduce three-dimensional relationships between two component measures and the outcome measure to two dimensions.

In order to measure the congruence between two constructs and how that affects the outcome, Jeff Edwards (2002) proposed polynomial regression and three-dimensional response surface methodology as a solution for the problem. Polynomial regression approach consists the difference and the higher order terms such as the quadratic terms and the interaction of two measures. The polynomial regression analysis also allows researchers to conceptualize the joint effects of the two constructs on an outcome as a three-dimensional surface.

Let us walk you through how to construct polynomial regression. There are a few steps we can follow:

• Fit in a linear model by using two construct measures (X & Y) as predictors and Z is the outcome. Calculate R Square and if R Square is not significant, we stop the procedure.

Z=b₀+b₁X+b₂Y+e

• If the R square is significant, then we added quadratic terms X² &Y² and interaction terms XY as set into the model. We test the increment in R Square and if the increment in R Square is not significant, we return back to the linear model.

Z=b₀+b₁X+b₂Y+ b₃X²+ b₄ XY+b₅Y²+e

• If the increment in R Square is significant, we added cubic terms X³, X²Y, XY² andY³. Again, we test the increment in R Square and if the increment in R Square is not significant, we return back to the quadratic model.

Z=b₀+b₁X+b₂Y+ b₃X²+ b₄ XY+b₅Y² b₆X³, b₇X²Y, b₈XY² + b₉Y³+e

After we established our model, now it is time to draw some fancy 3D response surface graphs. Jeff Edwards made the process very easy. You can download the Excel file for plotting response surfaces and plug in the coefficients of your model. The excel file will generate the graph automatically for you.

Here are some samples of the response surfaces graphs:

Linear:

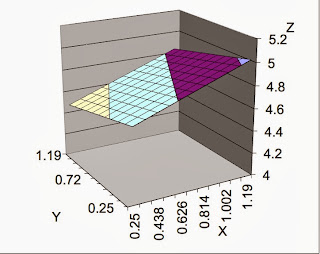
Quadratic:

Reference:

Edwards, J. R.  (1994).  The study of congruence in organizational behavior research: Critique and a proposed alternative.  Organizational Behavior and Human Decision Processes, 58, 51-100 (erratum, 58, 323-325).

Edwards, J. R.  (2002).  Alternatives to difference scores: Polynomial regression analysis and response surface methodology. In F. Drasgow & N. W. Schmitt (Eds.), Advances in measurement and data analysis (pp. 350-400).  San Francisco: Jossey-Bass.